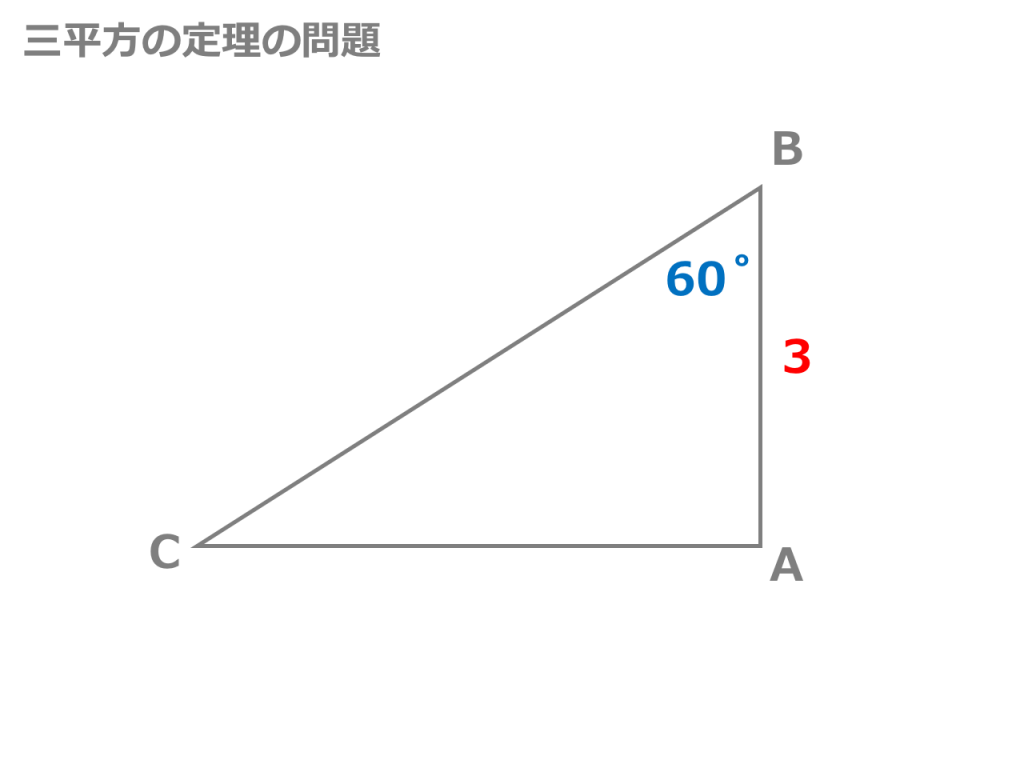
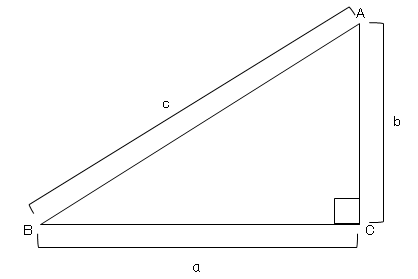
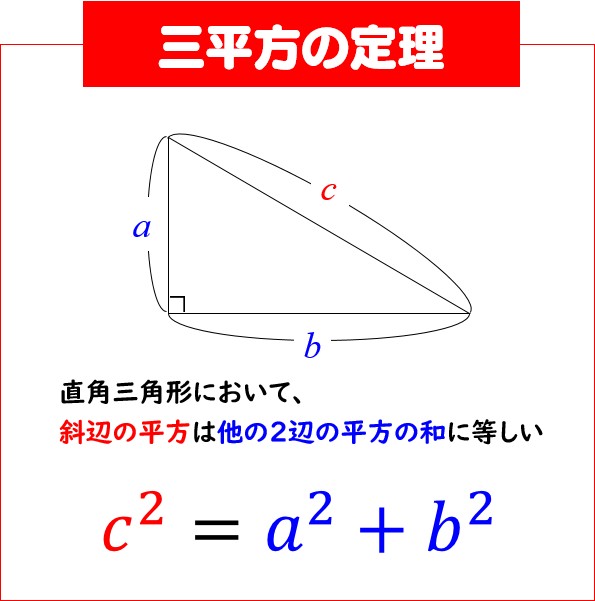
三平方の定理の公式を紹介します。下の図のように直角三角形の直角を挟む2辺をa,bとし、斜辺をcとすると a²b²=c² の等式が成立することを三平方の定理と言います。 三平方の定理の証明 三平方の定理の証明について紹介したいと思います。※三平方の定理を使える 直角三角形を見つける。 2辺がわかれば定理を使って残りの辺の長さを出す。 直角三角形は abdと acdの2つ。 2 2 acdはac=3, cd=1なので、 ad 2 1 2 =3 2 ad 2 =8 ad=±2 2 ad>0より ad=2 2 表示 すると abdでも2辺の長さが出たので 3 2 (2 2) 2 =x 2 x 2 =98 x重要 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b とし、斜辺の長さを c とすると、次の関係が成り立つ。 c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} この定理を証明したのは古代ギリシアの数学者ピタゴラスであるとも言われているので、この

三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく
三角形 直角 三平方の定理
三角形 直角 三平方の定理-② 三平方の定理を理解し,直角三角形の2辺の長さがわかっているとき,残りの辺の長さを求める。 評三平方の定理の意味を理解することができる。(発表,ノート) ③ 三平方の定理の逆について考え,その定理を利用して直角三角形を見つける。 ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。 直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c²



三平方の定理 スタディーx
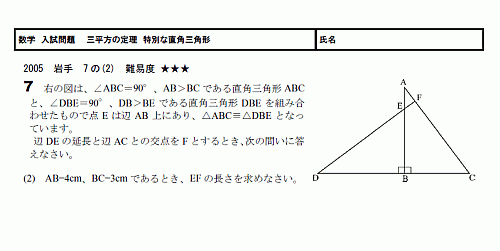
三平方の定理 上図のように,直角三角形ABCの直角を挟む2辺の長さを,a, b, 斜辺の長さを c とすると, 辺の長さの間に次の関係式が成り立つ。 これを,「三平方の定理」または「ピタゴラスの定理」という。 ※ 「斜辺」とは,直角に対する辺で,直角ありそう」 直角三角形の 「3つの正方形の1辺から三角形ができた」 理に気付けるようにする。 「どんな三角形でも三平方の定理は成り立つのか調 べてみたい」 「三平方の定理を知り,どんなときに使われて,どん な風に便利になるのか楽しみです。下の三平方の定理の証明の方法について,太郎さんと花子さんが考えています。あとの(1), (2)の各問いに答えなさい。 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b, 斜辺の長さをc とすると,次の関係が成り立つ。 a 2+ b = c
⑬外接円と直角二等辺三角形を利用した証明 外接円に4つの直角二等辺三角形を混ぜた図形から、証明を行います。 ⑭相似を利用した証明3 中学3年生レベルの円、相似の知識を使って三平方の定理を導いています。 ⑮教科書の証明特別な直角三角形は 三角定規の $\textcolor{blue}{2}$ 種類 になります。 ① $\textcolor{blue}{30°,60°,90°}$ POINT:正三角形の半分 正三角形の $1$ 辺の長さを②とすると、$1$ 辺はその半分なので①となります。残り $1$ 辺を三平方の定理を使って求めると、三平方の定理 空間図形での活用(1) 1 次の直方体について以下の問いに答え なさい。 3710 (1) 線分EGの長さを求めなさい。 EG=x ㎝とすると、 EFGは直角三角形 なので、三平方の定理より x =3+4 = x >0だから x = 答え
三平方の定理_座標平面の三角形 座標上の2点A,Bの距離 A (x1, y1),B (x2, y2)とすると 線分ABの長さ = (x 1 x 2) 2 (y 1 y 2) 2 A B x y O直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った /である直角三角形をかく。( 辺とその間の角を決めたので つに決まる)2 1 DE= とすれば、 、x は直角三角形なのでDEF 三平方の定理により ①a b x2 2 2+ = また、 において、仮定よ
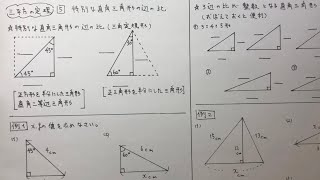



中3数学 三平方の定理5 特別な直角三角形の辺の比 すべて無料 星組の中学数学講座



1
中学数学 三平方の定理の内容 z 三平方の定理とその証明 z 直角三角形の辺の長さ z 三平方の定理の逆 z 三平方の定理の応用(平面図形、空間図形など) *「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方三平方の定理(ピタゴラスの定理) ∠ACB=90°となる直角三角形ABCにおいて,各辺の長さを, BC = a , CA = b , AB = c とすると, a 2 b 2 = c 2 の関係が成り立つ.この関係を 三平方の定理 あるいは ピタゴラスの定理 という. 証明




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学
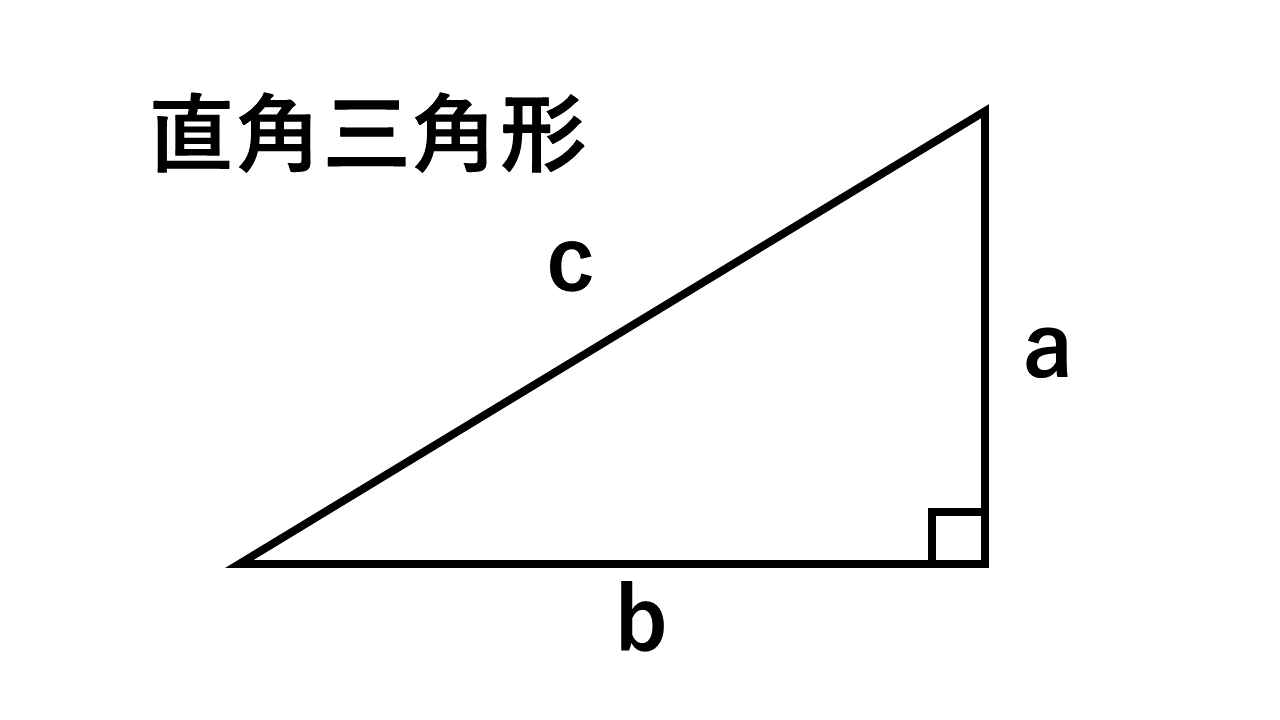
三平方の定理を使うと、直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます。 このページでは、三平方の定理を分かりやすく説明しています。中学校で学習する前の人にも、三平方の定理の意味を理解してもらえるような解説にしているので、ぜひお読みください。2 d geleden STEP1 三平方の定理とは 直角三角形ABCの辺ABの長さをc、辺ACの長さをb、辺BCの長さをaとします。 このとき、直角と向かい合う辺ABを斜辺といい、3 3:4:5の三角形で,本当に直角ができるのでしょうか。 三角形の辺の長さの比と角の大きさには,どんな関係があるのでしょうか。 3:4:5は,斜辺の対角が直角です。このことは,三平方の定理として知られています。 3:4:5




三平方の定理 覚えておきたい基本公式を解説 数スタ




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ
つまり「斜辺以外の二辺の長さの二乗の和」は「斜辺の二乗」と等しい。 a,b,c a,b,c は直角三角形の3辺の長さで,三角形の成立条件と距離の公理 上 計量ということ 前 計量ということ 三平方の定理 美樹 数学iで「図形と計量」という単元があります. 三角比の定義を習い,三角比を用いて長さや面積,体積を求めま三平方の定理 とはひとことでまとめると「 直角三角形の3辺の長さの関係を表す公式 」です。 上記のような公式が成り立ちます。直角三角形においてcを斜辺とします。すると、斜辺以外の2辺を2乗した数の和に等しいという公式です。



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs




三平方の定理 スタディーx
三平方の定理にはたくさんの証明方法があります。今回は外接円と直角二等辺三角形を利用した証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピ 三平方の定理とは、 「不思議な直角三角形」の不思議さを説明したもの です。 直角三角形は、上の図のような形をしていて、内側の 3 つの角のうち、 1 つが 90 度になっています。 90度(直角)を挟む辺の長さを b 、 c として、斜辺を a とすると、次の 1、等積変形に依る三平方の定理の証明 2、4枚の合同な直角三角形の配置の仕方に依る証明(これを1通りと観るかは人に依る。僕は4つ紹介はしたが) そして、今回のお話のテーマになる。 3、 直角三角形、三つ巴の世界




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Juniorhighschool Suugaku 3 6a Pdf
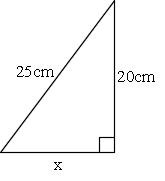
三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。 解き方 直角三角形に対し三平方の定理を使います。 (2)は直角三角形が無いですね。 補助線を引いて直角三角形を作ります。 そのうえで高さを求めていきます。 解説 (1)次の三角形のabの長さを求めなさい。No9 発展三平方の定理② 組 氏名 問1 次の長さを3辺とする三角形のうち,直角三角形はどれですか。 問2 3辺の長さが, , +2, +4である三角形が,直角三角形になるためには がどんな




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube
では直角三角形を図にしていきましょう。 sinは高さ/斜辺 なので、直角三角形の 高さ5,斜辺13 とわかります。 底辺は、 三平方の定理 を使えば、 a 2 b 2 =c 2 5 2 底辺 2 =13 2 底辺=12 とわかります。定理 直角三角形で、斜辺を直径とする半円が内接していて他の2辺を直径とする半円は外接している。 斜辺でない方の2辺の半円と直角三角形の和と斜辺の半円の面積の差は、元の直角三角形の面積と等しい。 つまり図では青と赤の面積が等しい。■次のような直角三角形の三辺の長さについては, a 2b 2=c 2 が成り立ちます.(これを三平方の定理といいます.) ■逆に,三辺の長さについて, a 2b 2=c 2 が成り立つとき,その三角形は直角三



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau
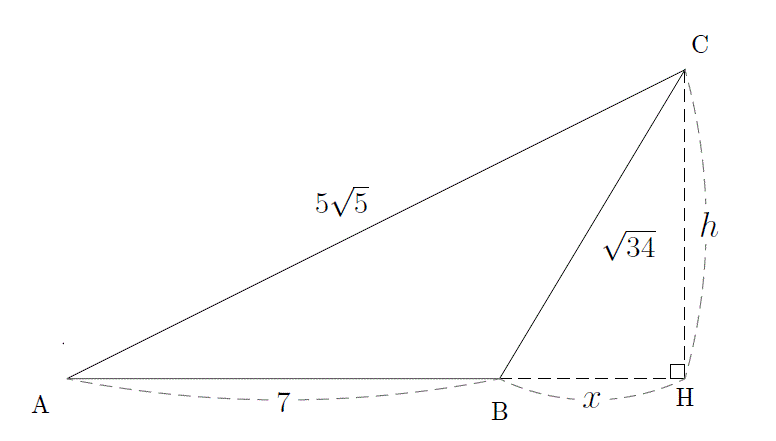



かみのドリル 三平方の定理
直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。三平方の定理を使うと、2点間の距離を求めることができます。2点の座標をそれぞれ(x 1, y 1)および(x 2, y 2)とし、2点間を結ぶ直線を斜辺とした直角二等辺三角形を考えます(図Math002)。すると、直角二等辺三角形の底辺が(x 1x 2)、高さが(y 1y 2)になります。よって、2点間の長さをlとしたとき三平方の定理は、直角三角形の3つの辺の長さの関係を表わした定理で、直角三角形の直角を挟む2つの辺の長さをそれぞれ a a 、 b b とし、斜辺の長さを c c とすると、 a2 b2 = c2 a 2 b 2 = c 2 の関係が成り立つ、という定理です。




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
直角二等辺三角形の辺の比は、必ず「 \color {red} {1 1 \sqrt {2}} 」 となります。 1 辺の長さからほかの辺の長さを簡単に求められるので、この比は必ず覚えておきましょう。 なぜこの比が成り立つかは、 三平方の定理 から示すことができます。 三平方の




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




โน ตของ 中学数学 三平方の定理のキホン ช น Junior Clear



三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか Yahoo 知恵袋
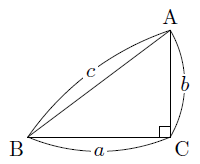



直角三角形の辺の長さ まなびの学園




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室




2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ
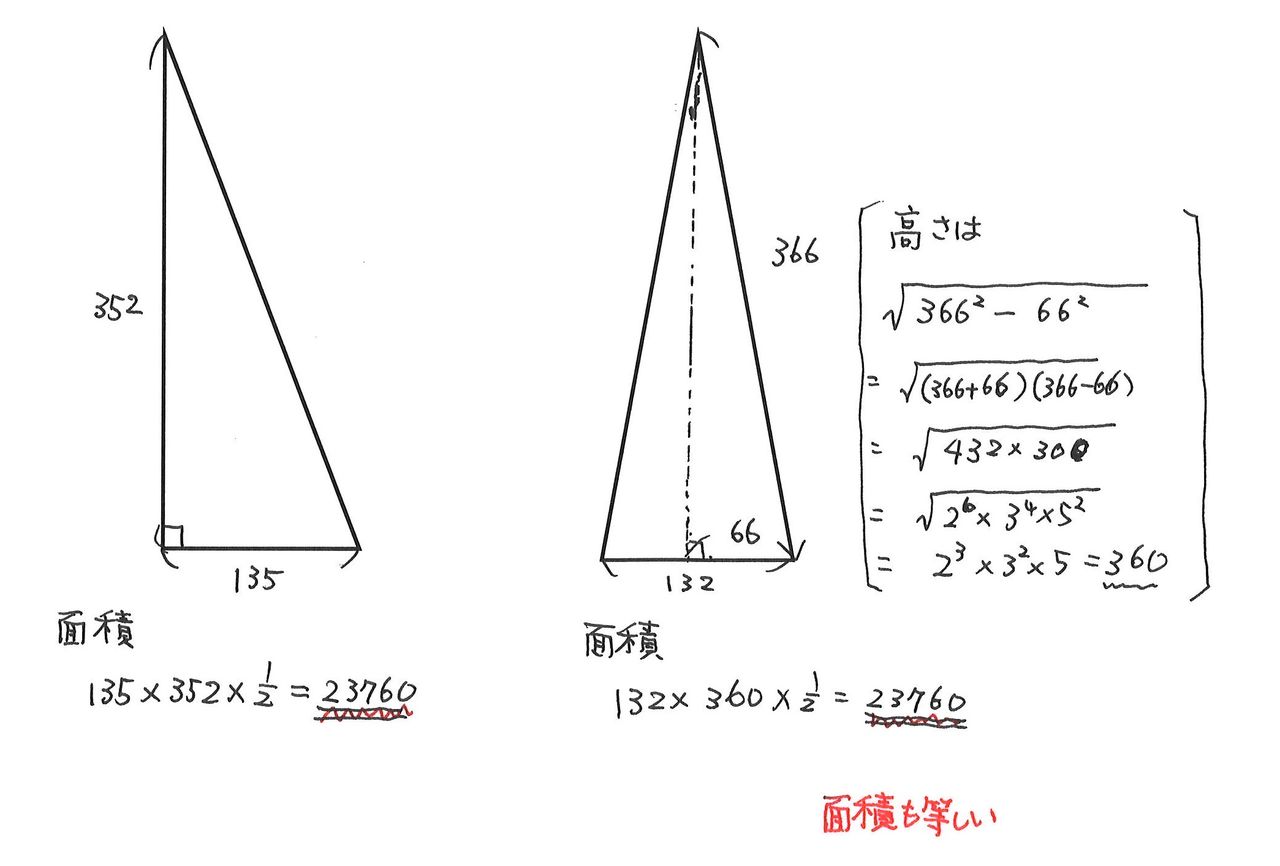



三角形のペア 大田 桐光本部校 ブログ




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




直角三角形 Wikipedia




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学
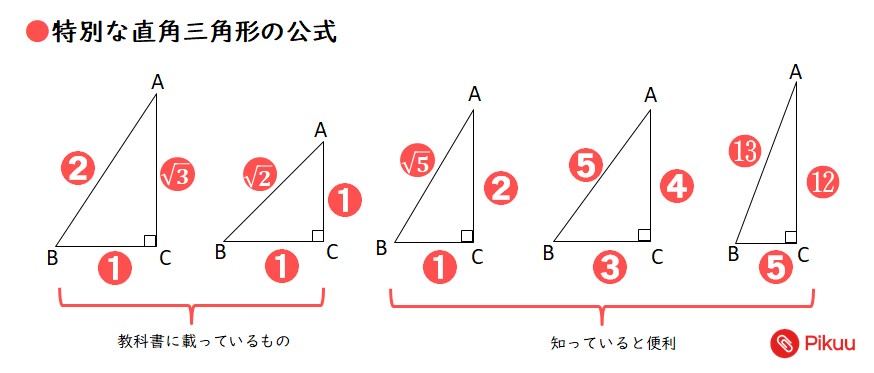



高校入試対策数学 特別な直角三角形を使った問題 Pikuu




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理 無料で使える中学学習プリント
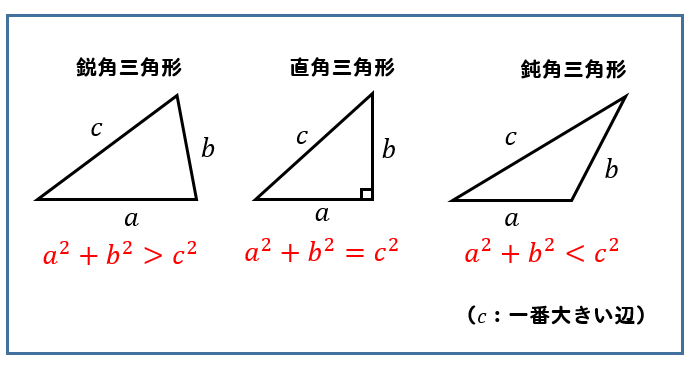



鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
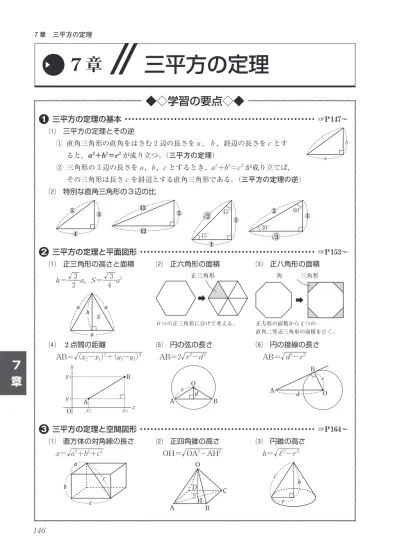



見本pdf 新中学問題集 発展編 塾用教材 教育開発出版株式会社 Scm H S3 Mihon




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理 ピタゴラスの定理




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理の証明と使い方



1
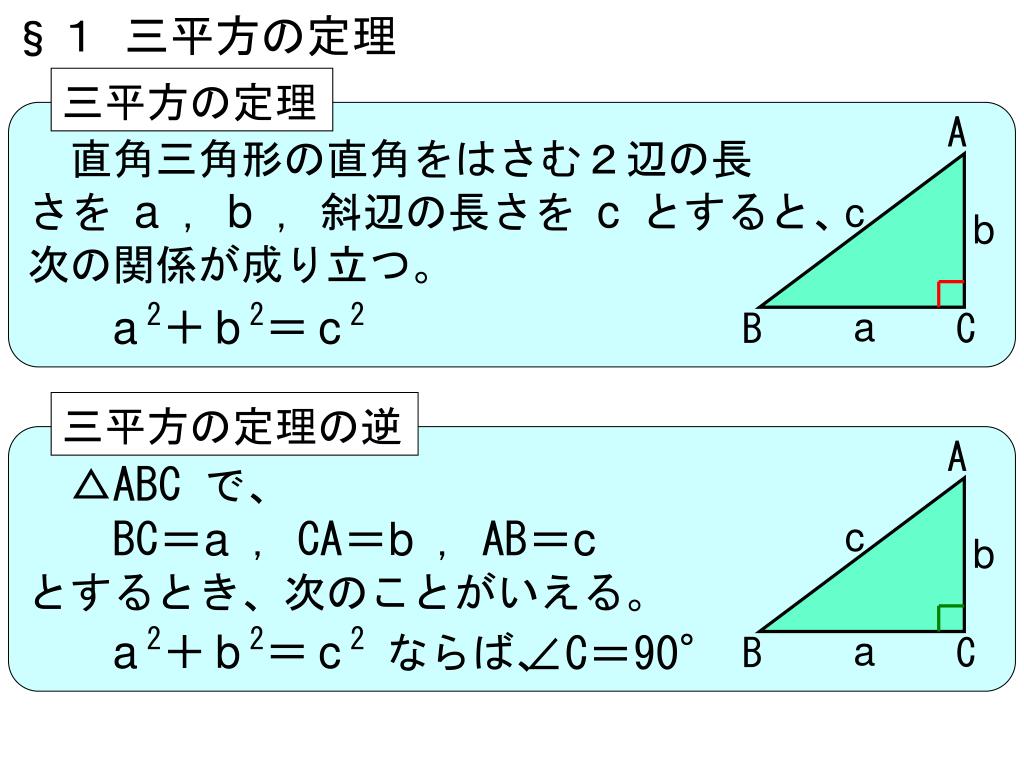



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋



三平方の定理




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理の証明と使い方




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド
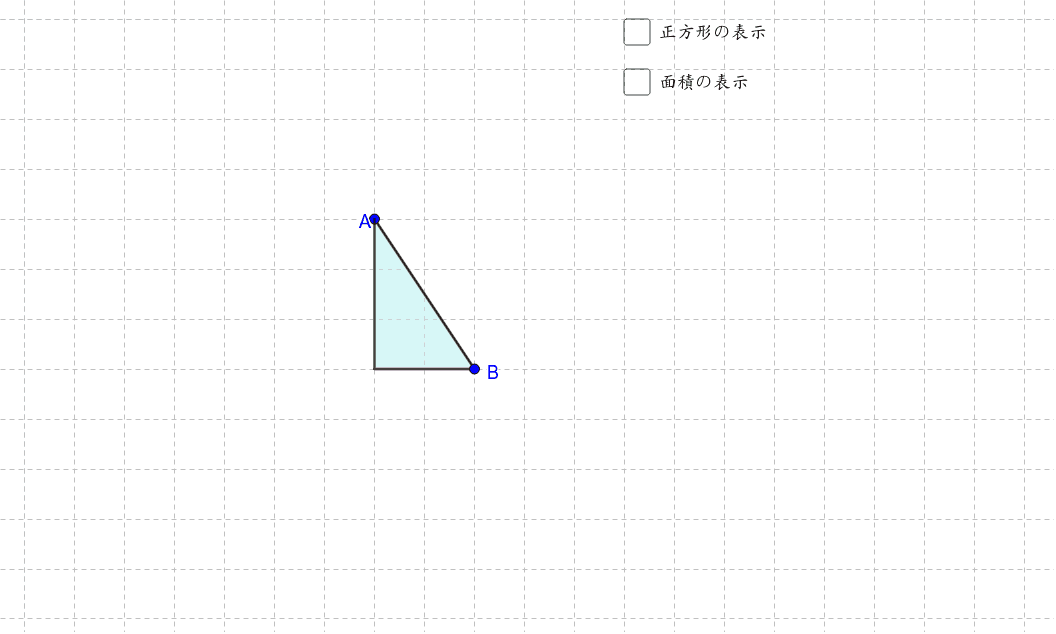



三平方の定理の導入 Geogebra



三平方の定理 1 ネット塾
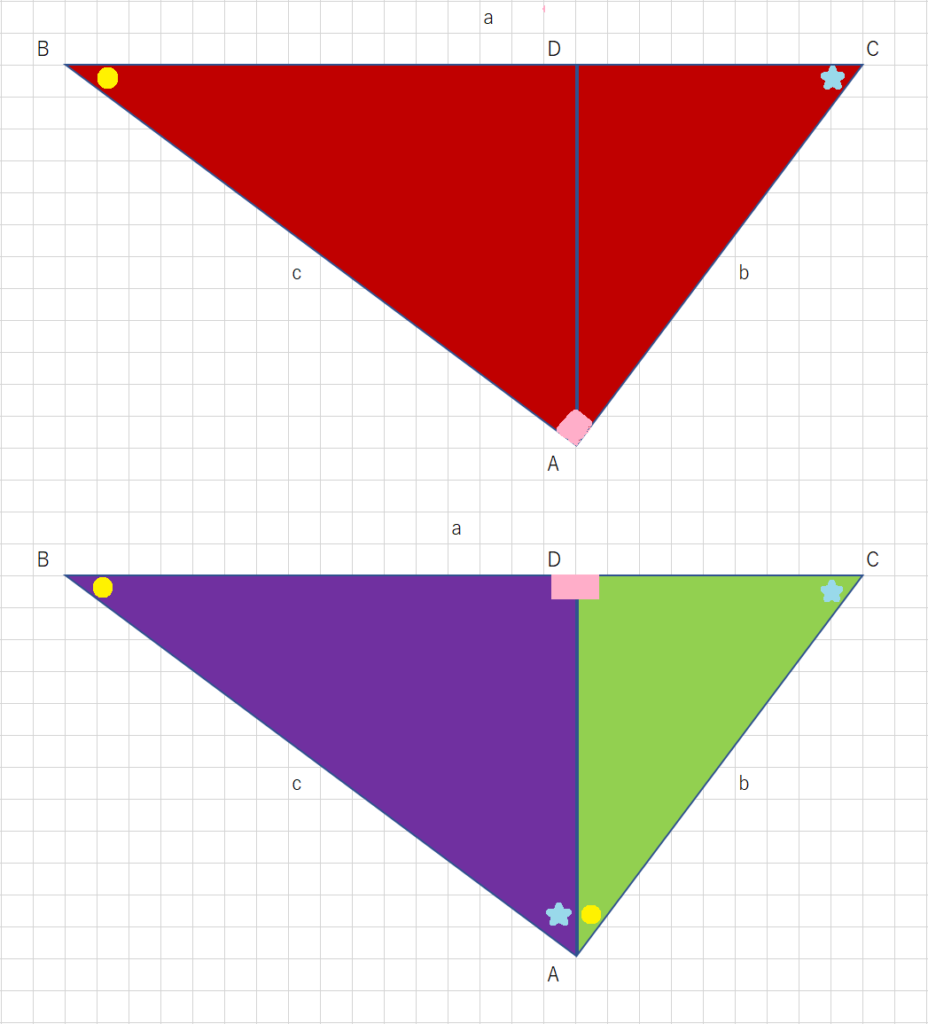



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理の応用




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも
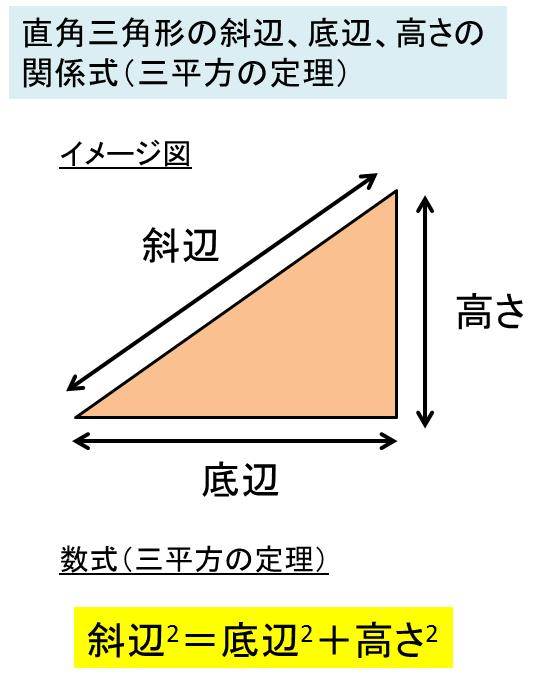



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方




三平方の定理の証明と使い方
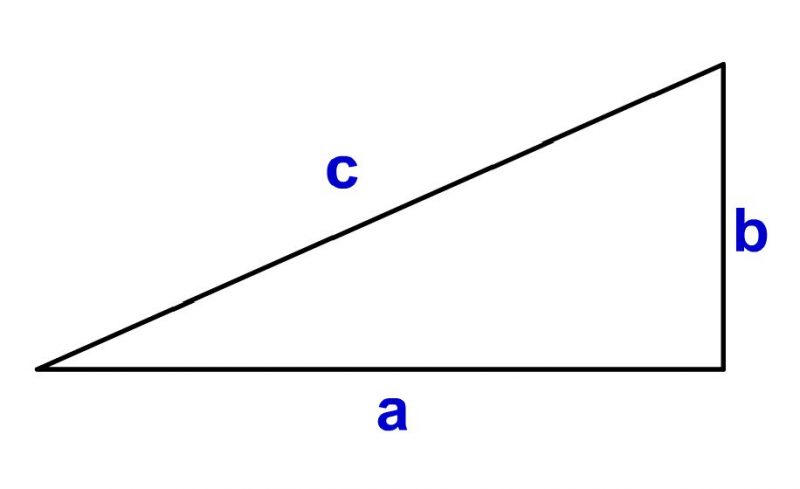



三平方の定理 をシミュレーションで復習しよう 数学入門




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三平方の定理の証明 直感的に分かる図で解説します 数学fun



三平方の定理




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



中学数学 直角三角形3 4 5以外に知ってる




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
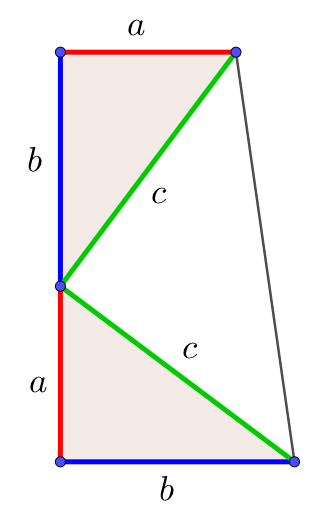



三平方の定理の証明3 大統領の台形 キソカラ




特別な直角三角形の3辺の比 の問題が分からないんですけど やり方を教えてください Clear




三平方の定理で辺を求める Youtube



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
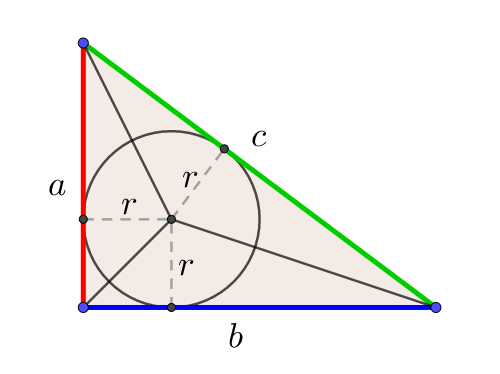



三平方の定理の証明4 直角三角形と内接円 キソカラ




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




数学 中3 61 三平方の定理 基本編 Youtube



三平方の定理 やややさしい数学




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




直角三角形の辺の長さ 合同条件 面積について アタリマエ




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 おやじさん ネット



1



高校入試 英語 数学 三平方の定理の逆



0 件のコメント:
コメントを投稿